Tourbillon est aussi un terme de la Philosophie de Descartes qui pretend qu’il y a dans le Ciel plusieurs revolutions d’astres autour de divers centres, qui font des sistemes differents, et pareils à celuy de notre region des Planètes.
Antoine Furetière1
1. Introduction
René Descartes (1596‑1650) s’est intéressé à l’astronomie dans le cadre de son vaste programme de refondation de la philosophie2. Au cours de l’été 1633, une grande étape de ce projet est achevée. Le philosophe français, qui n’a encore rien publié, vit isolé du monde aux Provinces-Unies. Il est en relation suivie avec les cercles savants français par le réseau épistolaire organisé par le père minime Marin Mersenne (1588‑1648)3. Toutefois, alors qu’il envisage d’éditer son livre, intitulé Le Monde4, il est informé du procès de Galilée (1564‑1642) et de la condamnation de l’astronome toscan par le Saint‑Office.
Dans une lettre à Mersenne, datée de la fin novembre 16335, Descartes fait part de son désarroi. Il ne connaît pas bien le déroulement du procès, mais suppose que ce l’on reproche à Galilée est d’avoir « sans doute voulu establir le mouvement de la Terre ». Il pensait que ce sujet – qui alimentait des débats depuis plusieurs décennies et qui « avait esté autresfois censuré par quelques Cardinaux » – ne posait plus vraiment problème. En fait, ces nouvelles mettent en cause tout son travail car, si ce mouvement « est faux, tous les fondemens de [sa] Philosophie le sont aussi ». Ne voulant pas être « desaprouvé de l’Eglise », il renonce à mettre sous presse son traité.
Descartes a tenu en grande partie parole. Du traité du Monde, il ne publie, en 1637 et sous le titre Discours de la méthode, que l’introduction, accompagnée de trois Essais de même origine6 ; ouvrage qui lui a assuré une immédiate célébrité. Plus tard, en 1644, dans Les Principes de la philosophie, il rend enfin publique, de manière plus détaillée, mais avec une certaine prudence, sa conception de la cosmologie. Le texte original est en latin. Il est édité peu après dans une traduction française réalisée par l’abbé Picot et supervisée par Descartes7. Le manuscrit du traité du Monde, pour sa part, n’a pas été détruit. Il a été imprimé en 1664, soit quatorze ans après la disparition de son auteur, par l’éditeur parisien Jacques Le Gras8.
Bien que Descartes ne fût pas un astronome, les développements cosmologiques que ces deux textes contiennent révèlent qu’il avait acquis de solides connaissances dans cette discipline, et qu’il était au courant des découvertes et des débats les plus récents. Mais, ce qui fait l’originalité et la grande portée de son entreprise, c’est qu’il intègre – bien plus que ne l’avait tenté Giordano Bruno (1548-1600)9 dans les années 1580-1590 – les préceptes de l’astronomie copernicienne dans une vaste conception du monde (au sens le plus large de cette expression), puisque non seulement elle englobe tous les champs de la science, mais encore elle les articule avec une métaphysique originale, en posant dans le même temps les fondements d’une nouvelle méthode rationnelle d’appréhension du réel10. De ce point de vue, il n’est pas faux de dire que, depuis Aristote (384-322 av. J.-C.), aucune entreprise d’une telle envergure n’avait été tentée.
Si, en introduisant cette étude, ce rappel général méritait d’être fait, l’objet de mon propos sera ici plus limité ; mon intervention s’inscrivant dans un programme collectif de recherche centré sur l’histoire de la notion de « système planétaire » et s’intéressant, dans le cas présent, à « l’engendrement du monde ; circulations des modalités génésiques du système solaire du xviie au xixe siècle »11, je me concentrerai donc sur les textes de Descartes qui se rapportent à la cosmologie – essentiellement Le Monde et les deuxième, troisième et quatrième parties des Principes de la philosophie – en étudiant plus spécifiquement comment Descartes conçoit la formation des systèmes planétaires et l’organisation cosmique qui en résulte : le système solaire en premier lieu, mais aussi les autres systèmes que postule sa théorie originale du cosmos.
Pour cela, et parce que la philosophie naturelle de Descartes est d’une grande cohérence et, surtout, parce qu’elle fusionne les domaines jusqu’alors distincts de la physique et de l’astronomie sous les mêmes principes, il sera préalablement nécessaire de bien définir ces derniers, en montrant quelles conséquences ils ont sur sa conception des tourbillons qui agitent l’univers en formant des systèmes planétaires. Il sera alors possible de se pencher sur leurs composantes principales – les étoiles, les planètes, les satellites, les comètes et le milieu dans lequel les astres évoluent –, en analysant leur formation, leur dynamique propre et, enfin, en s’interrogeant sur les interrelations qu’entretiennent des systèmes planétaires voisins.
Pour terminer ce préambule, je précise que si j’utilise les concepts familiers de « système solaire » et de « système planétaire », c’est, comme je me propose de le montrer, parce que, de fait, ces concepts sont à l’œuvre dans la cosmologie cartésienne, bien que n’étant pas employés sous cette forme verbale dans les textes étudiés12. Descartes utilise simplement à leur sujet le mot « ciel » ; chaque ciel étant organisé autour d’une étoile et, animé d’un mouvement tourbillonnaire qui entraîne l’ensemble des corps qu’il contient. S’agissant plus particulièrement du système solaire, Descartes le nomme « le premier ciel »13.
2. Une nouvelle physique qui concerne l’univers tout entier
Vers 1630, l’astronomie nouvelle, qu’elle s’appuie sur le système copernicien enrichi par les découvertes de Galilée, ou sur celui, hybride, conçu par Tycho Brahe (1546-1601), a accumulé de nombreuses données qui tendent à remettre en cause le postulat d’Aristote, repris dans l’enseignement scolastique, d’une différence de nature entre le monde sublunaire et le monde céleste. Cette coupure radicale de l’univers au niveau de l’orbe de la Lune conduisait les aristotéliciens et leurs disciples à lui consacrer deux sciences distinctes, la physique et l’astronomie, sans rapport l’une avec l’autre. Pour Descartes, au contraire, cette coupure n’a plus de raisons d’être : pour lui, l’astronomie devient une branche particulière d’une nouvelle physique qui concerne l’univers tout entier14.
L’univers cartésien, dans toutes ses composantes, célestes comme terrestres, est formé d’une matière unique15. Il n’est donc plus question des quatre éléments (terre, eau, air, feu) de la physique ancienne. Propres au monde sublunaire, ces derniers se distinguaient par leurs qualités, principalement par les couples antagoniques de chaud et de froid, de sec et d’humide, mais aussi de grave (lourd) et de léger – ces dernières qualités déterminant des mouvements naturels rectilignes et verticaux (respectivement vers le bas et vers le haut). Tandis que le ciel était composé d’un élément unique et immuable, l’éther ou quintessence, et que les corps célestes étaient animés de mouvements circulaires réguliers autour du centre terrestre du cosmos.
La matière cartésienne est identifiée à un espace géométrique « indéfini »16. Le système de Descartes se distingue ainsi non seulement de la cosmologie aristotélico-ptoléméenne qui clôturait l’univers au niveau de la sphère des étoiles fixes, mais également des systèmes de Copernic ou de Tycho Brahe qui conservaient une telle clôture. Il se rapproche de la conception de Giordano Bruno ; celle d’un univers infini. Toutefois, par prudence, mais aussi parce que ses principes méthodologiques interdisent au Français de spéculer sur une notion (l’infini) dont il ne peut se faire une idée physique précise, il adopte un point de vue qui laisse en suspens une telle hypothèse, sans l’écarter totalement : il considère que l’univers est indéfini ; ses limites ne pouvant être déterminées ni rationnellement ni expérimentalement.
De plus, en posant que la matière se confond avec l’espace, il en résulte qu’il n’y a pas de vide, et cela en aucun endroit du cosmos, fût-il infime17. Descartes conserve ici un principe fondamental de la philosophie naturelle aristotélicienne, mais en l’intégrant dans une conception de l’univers très différente.
La matière, selon Descartes, ne forme pas un bloc compact, elle se divise en un ensemble de corps de tailles et de formes variées. Cette divisibilité est à mettre en relation avec sa dynamique, elle aussi originale. Dieu, lors de la création, a donné à l’univers une certaine quantité de mouvement qui reste constante au cours des temps18. Il en résulte qu’un corps immobile demeure en cet état tant qu’il n’est pas heurté par un autre corps et que lorsqu’un autre corps le percute, son mouvement est rectiligne et la quantité de mouvement qui lui est transmise est égale à la quantité de mouvement que le corps qui l’a heurté a perdue19. C’est ce que la physique a retenu après Descartes sous le nom de « principe d’inertie » ; ce principe s’oppose tant à la théorie aristotélicienne qu’à celle de l’impetus des scolastiques, qui postulaient que le mouvement d’un corps tendait naturellement vers le repos20. Contrairement à la physique d’Aristote, les corps ne peuvent « naturellement » se déplacer, notamment pour rejoindre leur « lieu propre » du fait de leur « gravité » ou de leur « légèreté ». Cela a, comme nous le verrons, des conséquences pour expliquer les phénomènes liés à la pesanteur.
S’il existe un lien étroit entre la divisibilité de la matière et cette dynamique c’est que les corps en s’entrechoquant peuvent être amenés à se fractionner en plusieurs parties. D’autre part, dans cet univers qui n’accepte aucun vide, il faut que l’espace libéré par le déplacement du moindre corps soit immédiatement occupé par d’autres corps. Cela suppose que la matière puisse indéfiniment se diviser pour prendre les places infiniment petites qui assureront une jointure permanente entre le corps qui se déplace et le milieu ambiant21. Les corps microscopiques ou peu étendus ayant une plus grande fluidité sont qualifiés de « liquides » par Descartes, alors que les corps compacts de plus grande dimension correspondent à des corps « durs », soit ce que l’on désigne couramment comme des solides22.
Enfin, et en cela nous touchons à un aspect fondamental de la dynamique du cosmos : lors d’un impact, le corps percuté prend une direction naturellement rectiligne. Cependant, du fait qu’il évolue dans un milieu saturé de matière faisant obstacle à la direction initiale, son cours se trouve infléchi ; il suit alors une trajectoire courbe qui tend à prendre la forme circulaire23. Telle est l’origine de la structure tourbillonnaire de l’univers.
3. Les trois types de corps qui composent l’univers
Pour aller plus avant dans l’étude du cosmos en articulant celle-ci avec ses principes de physique, Descartes procède par analogie avec ce que l’on peut constater sur la Terre. En effet, puisque les mêmes phénomènes ont les mêmes propriétés, quel que soit l’endroit de l’univers où ils se produisent, il est légitime de généraliser les conclusions qu’on tire d’observations réalisées ici-bas en les rapportant à des phénomènes similaires constatés bien loin de notre monde.
La genèse de l’univers s’est trouvée décrite de deux manières différentes dans Le Monde et dans les Principes.
Dans Le Monde, Descartes suppose que, lors de la création, la matière a reçu de Dieu une « action » – ou « force de se mouvoir et de se diviser » – qui a mis l’ensemble de l’univers en mouvement24. Cet ébranlement initial n’aurait pas affecté de manière égale toutes les parties de l’espace. Aussi ajoute-t-il deux précisions. La première concerne le mouvement des parties de matière : « Et toutesfois, à cause que nous supposons que Dieu les a mues d’abord diversement, nous ne devons pas penser qu’elles se soient toutes accordées à tourner autour d’un seul centre, mais autour de plusieurs differens, et que nous pouvons imaginer diversement situez les uns à l’égard des autres.25 » La seconde se rapporte au fractionnement de la matière : « D’autant que nous supposons que Dieu a mis au commencement toute sorte d’inégalité entre les parties de cette Matière, nous devons penser, qu’il en a eu pour lors de toutes sortes de grosseurs et figures, et de disposées à se mouvoir, ou ne se mouvoir pas, en toutes façons et en tous sens26. » Ajoutons que, dès ce moment fondateur, Dieu a mû chaque partie de matière « autour de son centre »27. Cette situation quelque peu chaotique, mais déjà tourbillonnaire, a évolué en simplifiant, en fonction de la grosseur des différents corps, le positionnement de ces derniers à l’intérieur des tourbillons, en érodant les parties anguleuses lors des chocs ; processus qui a abouti à un univers composé de trois ensembles de corps, ou « éléments »28. C’est ainsi que se manifesterait désormais la matière en mouvement.
Dans les Principes, après avoir précisé qu’il n’est pas assuré que les causes qu’il propose « sont vrayes »29, il renonce à ce premier schéma cosmogénique, « à cause qu’il ne convient pas si bien à la souveraine perfection qui est en Dieu, de le faire auteur de la confusion que de l’ordre ». Il suppose « que toutes les parties de la matiere ont au commencement esté égales entr’elles, tant en grandeur qu’en mouvement ». Il admet cependant comme seule « inégalité en l’univers […] celle qui est en la situation des Estoiles fixes ». Sans s’étendre sur le sujet, il ajoute : « Au reste, il importe fort peu de quelle façon je suppose icy que la matière ait esté disposée au commencement, puis que sa disposition doit par apres estre changée, suivant les loix de la nature »30. En restant donc dans un certain vague, il peut ainsi retrouver la tripartition des « éléments »31, c’est-à-dire des trois catégories de corps postulées dans Le Monde et qu’on trouve actuellement dans le cosmos.
La distinction entre ces éléments est assez sommaire : le premier est constitué de particules très fines ; le deuxième, de corps de grandeur « médiocre », et le troisième, de corps de grande dimension. Or, en s’appuyant sur les observations des astronomes, il distingue trois grandes catégories de corps célestes : « Si nous considerons generalement tous les corps dont l’Univers est composé, nous n’en trouverons que de trois sortes […] : c’est à sçavoir le Soleil et les Etoiles fixes, pour la premiere, les Cieux pour la seconde, et la Terre avec les Planetes et les Cometes pour la troisième.32 » C’est ainsi que le philosophe est conduit à rattacher le Soleil et les étoiles d’une part, les « Cieux » d’une autre et enfin la Terre, les planètes et les comètes, aux trois types d’éléments constitutifs de l’univers.
Considérons tout d’abord, le Soleil et les étoiles33. Pour Descartes, ils présentent les mêmes caractères que la flamme. Ils sont formés d’une « liqueur, la plus subtile et la plus penetrante qui soit au Monde », dont les parties « se remuent beaucoup plus viste, qu’aucune de celles des autres corps »34. Ce fluide n’est rien d’autre que le « premier élément » de la physique cartésienne. Il est composé de particules infimes, soumises à une agitation permanente et d’une grande vélocité. Descartes explique sa formation en disant qu’il s’agit d’une « raclure qui a deu estre separée des autres parties de la matiere »35, lors des chocs subis par de plus grands corps. Ces particules, n’ayant « aucune grosseur ni figure determinée, remplissent aisement tous les petits angles ou recoins par où les autres parties de la matiere ne peuvent passer »36.
Lorsque Descartes parle dans un tel contexte des « Cieux », c’est pour désigner, non pas les tourbillons – qu’il nomme également des « cieux » – mais l’ensemble des corps matériels qui baignent l’espace entre les étoiles et les planètes. Nous le qualifierions aujourd’hui d’espace interplanétaire. Ce dernier est principalement constitué du « second élément ». La figure des corps qui le composent était irrégulière et anguleuse lors de l’impulsion initiale, mais, par la suite, à l’intérieur des tourbillons en formation, les parties saillantes se sont détachées quand se heurtaient ces amas de matière. Ils ont eu ainsi tendance à s’arrondir. De la sorte, les « cieux » sont devenus un amas de parties « rondes et fort petites ». Dans les interstices entre ces boulettes de matière se nichent des particules du premier élément. Cet espace, du fait de la rotondité des parties du second élément et de l’extrême ténuité de celles du premier élément qui comblent les vides, a donc une consistance fluide, « liquide » pour parler comme Descartes37.
Enfin, un « troisième élément », formé des corps les plus étendus, mais aussi les plus durs, est à l’origine des planètes et des comètes. Elles sont de faible célérité car « à cause de leur grosseur et de leurs figures [ces formes] ne pourront pas estre meuës si aisément que les precedentes »38. Aussi lors des chocs qu’elles ont reçus ne se sont-elles émoussées qu’en surface, ce qui leur a donné une forme vaguement sphérique.
Tels sont les objets théoriques essentiels sur lesquels repose la conception cartésienne de l’univers. Résumons ces données sous forme de tableau39 :
Tab. 1. Les objets essentiels dans la conception cartésienne de l’univers
(J. Lamy)
4. Genèse, formation et disparition des étoiles
Pour comprendre la formation des étoiles qui, à l’exemple du Soleil, se sont trouvées en position centrale, Descartes se sert d’une comparaison avec un phénomène physique que l’on peut facilement expérimenter (schémas 1 et 2)40. Après avoir expliqué que, dans une fronde, « ce qui fait tendre la corde d’autant plus fort » est « qu’on la fait tourner plus vite » et que « ce qui fait tendre cette corde, n’est autre chose que la force dont la pierre fait effort pour s’éloigner du centre autour duquel elle est meuë41 », il imagine sur ce modèle une boule (2-A) incluse dans un tuyau (2-EY), lui-même tenu à une extrémité et agité comme une fronde. Du fait de la rotation rapide du tube, la boule roule à l’intérieur de celui-ci du centre vers l’autre extrémité avant d’être projetée au-dehors. Et comme il n’y a pas de vide dans la nature, la place libérée dans l’autre partie du tuyau, occupée initialement par la boule, a été instantanément remplacée par de l’air, plus ténu et fluide, qui s’est dirigé vers le centre du mouvement circulaire.
Si l’on fait une analogie entre cette expérience et un tourbillon cosmique, l’on peut supposer que la force centrifuge tend à éloigner du centre du tourbillon les corps les plus massifs et, en conséquence logique, dans cette physique non vacuiste, à amener les corps les plus petits vers le centre. Cette démonstration, transposée dans l’espace par Descartes, en mettant en jeu les corps du premier et du second élément, peut se formuler ainsi : la dynamique propre des tourbillons rassemble en leur centre la matière du premier élément, qui forme ainsi une étoile comme le Soleil, et place à sa périphérie la matière liquide de l’espace cosmique, autrement dit le second élément.
Descartes, dans son étude des étoiles, se concentre sur l’exemple qui est le plus facilement observable : le Soleil. Cela le conduit à s’intéresser longuement aux taches solaires42, phénomène qui, depuis Galilée et d’autres savants comme le père jésuite Christophe Scheiner (1575-1650) qu’il utilise tout particulièrement43, suscite maintes interrogations. Pour expliquer leur formation, il recourt, là encore, à une comparaison : celle du Soleil et d’une liqueur qu’on fait bouillir et à la surface de laquelle se forme une écume. Par analogie, il suppose que dans une étoile, quelques parties du premier élément, parmi les moins fines et les moins arrondies, ont tendance à s’assembler à la surface de l’astre. Moins lumineuses, elles s’agglomèrent en une couche qui obscurcit la zone où elles se sont engendrées. Il s’agit de formations instables, qui apparaissent, se déplacent et finissent par disparaître, avant de resurgir à un autre endroit.
Certains corps qui composent ces taches retournent en effet dans le cœur de l’étoile, après avoir été fractionnés en particules plus petites, d’autres forment à la périphérie de l’étoile une sorte d’« air », qui s’étend depuis la surface jusqu’aux abords de l’orbite de Mercure44. Descartes décrit ici la « couronne solaire » pour parler comme de nos jours.
Toutefois, il peut se produire que la tache prenne tant de consistance et d’extension qu’elle en vienne à couvrir entièrement la surface de l’étoile, la faisant disparaître à notre vue. Ou bien qu’une étoile qui se trouvait dans cette situation redevienne éclatante lorsque la couche qui l’obscurcissait a été rompue par l’agitation interne du premier élément. Tel serait l’explication des novæ, qui ont intrigué les savants comme Tycho Brahe et Johannes Kepler (1571-1630). Une nova ne serait donc pas pour lui à proprement parler une « nouvelle étoile », mais simplement une étoile, dont la tache qui en obscurcissait la surface s’est rompue, la rendant ainsi visible depuis la Terre.
Dans le cas inverse, il peut se produire que la tache devienne si compacte et qu’elle s’accroisse tant en volume qu’elle en vienne à occuper le cœur même de l’étoile en agglomérant progressivement toutes ses parties. En perdant la consistance du premier élément, c’est-à-dire la ténuité et la célérité des particules qui le composent, et en formant un corps solide et peu mobile, autrement dit un corps du troisième élément, l’étoile ainsi transformée en planète (ou en comète), perturbe toute la dynamique du tourbillon, où elle trônait en position centrale. Celui-ci perd de sa force et finit par être absorbé par les tourbillons voisins plus puissants.
5. Formation et dynamique des planètes, de leurs satellites et des comètes
Les corps massifs des planètes et des comètes, autrement dit les astres formés du troisième élément, peuvent ainsi trouver leur origine dans l’extinction de certaines étoiles. Toutefois, Descartes postule que la plupart d’entre elles auraient eu cette configuration dès la création et n’ont été ensuite que peu altérées par le choc avec d’autres corps. D’autres, enfin, se sont formées par la jonction de corps déjà assez gros, qui se sont rencontrés sans se briser et sont restés accrochés ensemble en formant des planètes plus volumineuses45.
Pour le philosophe, du fait de leur massivité – c’est-à-dire, ceux « ayant plus de superficie »46 –, les planètes opposent une grande force « pour résister »47, qui n’affecte que peu leur état. Elles ne sont pas immobiles pour autant. À l’intérieur d’un tourbillon, elles baignent en différents endroits de celui-ci dans le second élément. Faisant la comparaison avec un cours d’eau qui charrie des corps flottants48, les planètes à l’exemple de ces derniers, sont entraînées dans le flot tourbillonnaire du second élément49, et tournent de ce fait autour d’une étoile centrale, sans notablement être déplacées de leur orbite.
Le relatif équilibre de leur orbite en un lieu déterminé s’expliquerait par les caractères de chaque planète et de sa dynamique propre50. Freinée par la résistance que lui opposent les corps du second élément qui se trouvent dans la périphérie du tourbillon, la planète tend à incurver son mouvement vers le centre de celui-ci. Toutefois, arrivée dans une certaine zone, elle rencontre l’agitation des corps du premier élément qui dominent au fur et à mesure qu’on se rapproche de l’étoile centrale. Elle se trouve alors repoussée vers l’extérieur. Elle se voit ainsi confinée dans la partie de l’espace où s’équilibrent les deux forces contradictoires qu’elle subit : celle, centripète, de l’inertie du second élément extérieur et celle, centrifuge, de l’agitation du premier élément central51. C’est dans cette zone intermédiaire qu’elle stabilise sa révolution selon une orbite qui, du fait des contraintes diverses qui s’exercent sur les différents endroits du tourbillon, ne suit pas nécessairement une trajectoire circulaire52.
Il résulte de ce constat que les planètes les plus massives, celles qui par leur inertie vainquent plus facilement les forces de résistance du second élément, sont reléguées dans les parties les plus éloignées du centre, les moins massives en étant les plus proches53. Cela se vérifie dans le système solaire, à condition, d’admettre – comme le fait Descartes qui n’ignore pas que Mars est moins volumineux que la Terre, bien qu’ayant une orbite plus extérieure – que volume et quantité de matière d’un corps ne signifient pas la même chose. En effet, les corps solides (comme on le constate sur la Terre) peuvent être poreux. Leur volume s’en trouve augmenté d’autant, en regard de ce qu’il serait si la consistance des planètes était totalement compacte54. Quant à leur différence de vitesse de révolution, elle serait à mettre en rapport direct avec leur proximité du centre stellaire et de sa forte agitation qui accroîtrait leur célérité55.
Postulant un univers où la matière n’a ni gravité ni légèreté, Descartes se doit d’apporter une explication à la chute des corps. Pour lui, la pesanteur n’est pas une qualité intrinsèque de la matière, puisque celle-ci est uniforme. Dans Le Monde, il attribue ce phénomène observable sur la Terre au fait que « les parties du petit Ciel qui l’environne [autrement dit : principalement les boulettes du second élément] tournant beaucoup plus vite que les siennes autour de son centre, tendent aussi avec plus de force à s’en éloigner, et par conséquent les y repoussent »56. Il modifie légèrement sa théorie dans les Principes. Sans écarter totalement la force centrifuge, qui éloigne les particules plus petites et plus rapides du centre, il insiste sur la pression qu’exerce le milieu ambiant sur la planète du fait de son déplacement et de sa rotation autour de son axe. La matière qui environne celle-ci, de la même manière qu’elle tend à l’arrondir, « pousse également toutes les parties de sa superficie vers son centre » et « pousse aussi vers elle tous les corps qu’on nomme pesans »57. Il en résulte une expulsion des particules du premier élément présentes dans les pores et cavités intérieures de la planète et une chute concomitante des corps les plus compacts. De telles explications peuvent paraître contradictoires avec ce qui se passe à l’échelle d’un tourbillon tout entier, puisque, Descartes y ramène vers le centre les particules les plus petites et renvoie à la périphérie les plus grosses. Conscient de cette contradiction, il objecte que, dans un tourbillon, les corps massifs
« se mouvaient déja auparavant de mesme branle que la matiere de ce Ciel. Car il est certain que, s’ils n’ont point commencé à se mouvoir, ou s’ils se meuvent, pourveu que ce soit moins vite qu’il n’est requis pour suivre le cours de cette matiere, ils doivent d’abord estre chassez par elle vers le centre autour duquel elle tourne »58.
Descartes estime que dans certaines circonstances, il pourrait se former des tourbillons secondaires à l’intérieur d’un tourbillon principal centré sur une étoile59. Un tel phénomène peut communément être observé dans une rivière, où divers objets flottants entrent en rotation autour d’un vortex, tout en étant poussés par la puissance du courant principal. Il peut donc, du fait de l’universalité des lois physiques, être transposé dans le cosmos.
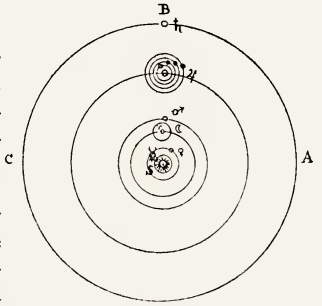
Quelle est l’origine de ces tourbillons secondaires ? Descartes émet l’hypothèse que le « premier ciel » (le système solaire) « a autrefois esté divisé en quatorze tourbillons, ou en davantage »60. Le premier de ces quatorze tourbillons est centré sur le Soleil, mais s’y ajoutent ceux centrés sur les six planètes alors connues (Terre comprise), ainsi que sur la Lune, les quatre satellites de Jupiter identifié et les deux de Saturne que l’on croyait avoir observés. Se dessine ainsi, à l’intérieur de chaque tourbillon formé par une étoile, une structure tourbillonnaire complexe à trois niveaux, puisqu’en son sein chaque planète anime un tourbillon et que de celui-ci peuvent dépendre un ou plusieurs tourbillons occasionnés par l’éventuelle existence de satellites. On remarquera que si, par prudence, les Principes ne s’intéressent qu’au système solaire, le traité du Monde montre que Descartes en son for intérieur étendait ces considérations aux autres tourbillons stellaires61.
En utilisant l’adverbe « autrefois », Descartes reste vague sur la naissance de ces tourbillons. Faut-il entendre dès la création de l’univers et du choc divin initial ? Dans certains cas, oui. À l’exemple d’une « pirouette » (une toupie) qui, du fait de son inertie, peut conserver très longtemps un mouvement de rotation autour de son axe, les planètes auraient pu faire de même durant « cinq à six mille ans » (âge du monde estimé couramment depuis la Création)62. Mais cette liste ne doit pas être considérée comme exhaustive. Certaines étoiles mortes se seraient aussi transformées en planètes sans avoir totalement cessé d’être en rotation autour de leur centre63, tandis que certains tourbillons peu puissants auraient, à cause de forces contraires, pu être totalement annihilés64. Le Soleil, par sa force, aurait ainsi entraîné les tourbillons voisins dans son sillage. Certains, dont on ne garde plus de traces, auraient totalement disparu. Les six planètes auraient conservé une activité tourbillonnaire autonome telle que les trois plus massives auraient été capables d’entraîner non seulement les boulettes voisines du second élément, mais encore, les corps plus volumineux de petites planètes se trouvant à proximité, en les transformant en satellites.
Descartes explique de la sorte l’existence de systèmes planétaires secondaires centrés sur une planète. Il en existe un autour de la Terre ; il est limité à la seule Lune. Galilée en a découvert un autre constitué de Jupiter et des quatre « astres médicéens » qui gravitent autour de lui. Quant à Saturne, Descartes se contente d’émettre l’hypothèse qu’un tel système pourrait expliquer les protubérances qui apparaissaient de part et d’autre de la planète65. En 1659, neuf ans après la disparition du Français, Huygens a montré que ces deux prétendus satellites de Saturne n’étaient en fait que l’apparence prise par un anneau lors de certaines observations avec des télescopes de faible grossissement. Quant aux satellites, Saturne en possède également, Huygens a découvert le premier, Titan, en 1655, mais, là encore après la mort du Français.
Fig. 2. Le « premier ciel » cartésien
(Principia, III, § 31, AT, VIII, p. 93)
Ce schéma met bien en évidence comment Descartes, figurant le « premier ciel », le conçoit comme l’emboîtement de trois types de tourbillons. Le principal (qui correspond au système solaire) est centré sur le Soleil ; les 6 planètes (Terre comprise) sont chacune le centre d’un deuxième type de tourbillon, quant à leurs satellites, chacun commande un troisième type. À la différence des deux autres types, les tourbillons des satellites n’entraînent pas de corps du troisième élément, mais seulement ceux du premier et du deuxième.
Alors que dans son développement décrivant le premier ciel, Descartes fait état de 14 tourbillons, ce qui sous-entend qu’il considère que les protubérances autour de Saturne seraient deux satellites, centre de deux tourbillons de niveau 3, son schéma qui ne les figure pas semble témoigner d’une certaine hésitation à ce sujet : état de la perplexité du monde savant de son époque sur un phénomène observé depuis Galilée, mais encore inexpliqué ?
Un autre phénomène, qui a beaucoup intrigué les savants, trouve une place originale dans la manière dont Descartes envisage les systèmes planétaires dans le cadre de sa cosmologie : il s’agit des comètes66.
Les comètes, comme les planètes, sont des corps qui, du fait de leur grosseur, se sont retrouvés repoussés vers la limite d’un tourbillon et, à cause de leur inertie, ont pu aisément s’introduire dans un tourbillon voisin et passer ainsi de la périphérie d’un tourbillon à celle de plusieurs autres.
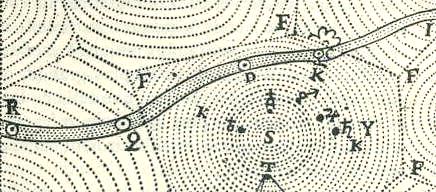
Fig. 3. Trajectoire d’une comète traversant plusieurs tourbillons
Le tourbillon centré sur S est le système solaire comme en témoignent les symboles des planètes (Le Monde, ch. VIII, AT, p. 55, détail)
Au cours de ces changements de tourbillon, les heurts qui se produisent avec des particules de matière empruntant des parcours différents ont tendance, d’une part, à faire perdre de la matière à la comète et, d’autre part, à modifier sa vitesse. Elle se trouve ainsi ralentie lors de la traversée des limites du tourbillon et de son entrée dans un autre, en raison des forces contraires qui s’exercent sur elle à ce moment-là. Mais, une fois intégrée dans le flot du nouveau tourbillon elle se meut plus rapidement, étant transportée par celui-ci, tout en conservant une grande partie de son mouvement initial. Cela explique qu’elle n’effectue pas, comme une simple planète, une révolution autour de sa nouvelle étoile et qu’elle ne soit présente que pendant un temps limité dans un ciel avant de passer dans un autre. Elle disparaît alors des observateurs qui se trouvent dans le ciel qu’elle a quitté.
Rappelons qu’au temps de Descartes, si l’on ne place plus les comètes dans la catégorie des météores, c’est-à-dire des phénomènes qui se déroulent dans les sphères supérieures du monde sublunaire, on les considère encore comme des phénomènes célestes transitoires, en donnant, depuis Tycho Brahe, à leur parcours la courbure d’un segment d’ovale. La théorie de Descartes est donc une tentative pour concilier ces enseignements récents de l’astronomie avec sa structure tourbillonnaire du cosmos. Toutefois, comme le remarque Charles Adam, Descartes
« se montre […] beaucoup plus hardi que Tycho lui-même. Celui-ci s’était contenté de démontrer que ce ne pouvait être des phénomènes sublunaires […] ; mais il ne les plaçait pas plus loin que la sphère de Vénus ou de Mercure. Il n’a pas osé, dit Descartes, leur attribuer toute la hauteur qu’il découvrait »67.
6. Conclusion
Tels sont, brièvement résumés et en laissant de côté de nombreux détails que Descartes développe avec minutie dans Les Principes de la philosophie, les grandes caractéristiques de ces « cieux » tourbillonnaires qui entraînent autour d’une étoile centrale la matière interplanétaire ainsi que les planètes, leurs satellites et les comètes : bref, de ces objets célestes complexes que l’astronomie nouvelle commence à baptiser « systèmes planétaires ».
La première force de la théorie cartésienne est, comme cela a été dit en introduction, d’offrir une conception unifiée de toute la philosophie naturelle, en plaçant sous les mêmes principes et les mêmes lois les phénomènes que la physique cantonnait traditionnellement dans le monde sublunaire et ceux qui relevaient plus spécifiquement de l’astronomie. En second lieu, les savants qui, depuis la Renaissance, enregistraient les faiblesses et les insuffisances de la science scolastique, pouvaient grâce à lui, disposer d’une alternative capable de rivaliser avec le monumental système hérité d’Aristote et complété par Ptolémée. Enfin, l’ambitieuse tentative de Descartes avait le grand mérite d’apporter une réponse aux nombreuses questions que posait la science moderne en plein développement et d’offrir aux savants novateurs un cadre conceptuel et problématique capable d’intégrer les découvertes à venir.
Tout cela était de nature à donner aux travaux du philosophe français un grand rayonnement international ; ce qui ne manqua pas d’arriver. Toutefois, en dépit de son souci constant d’ancrer ses développements théoriques dans le réel, le système du monde de Descartes et, à l’intérieur de celui-ci, sa théorie des systèmes planétaires reposaient sur beaucoup d’hypothèses invérifiables par la science de son temps. Ils reposaient également sur des postulats physiques tout aussi fragiles.
Deux d’entre eux ne tardèrent pas à être remis en cause peu après la disparition du philosophe, ébranlant par là même tout son édifice cosmologique. Le premier l’a été par la mise en évidence de l’existence du vide par les expériences d’Evangelista Torricelli (1608-1647), de Blaise Pascal (1623-1662) et d’Otto von Guericke (1602-1686). Cela ruinait sa conception d’un univers plein d’une matière unique. Or, et là est sa seconde faiblesse, la dynamique cartésienne se proclamait a priori comme radicalement mécaniste. Sans la pression directe d’un autre corps matériel, un corps immobile ne pouvait être déplacé. Descartes, comme Galilée et tous les mécanistes qui leur emboîtèrent le pas à l’exemple de Jacques Rohault (1618-1672), Pierre Sylvain Régis (1632–1707) et Bernard Le Bouyer de Fontenelle (1657-1757), était un adversaire déclaré de l’hermétisme, qui avait trouvé tant de partisans à la Renaissance et qui conservait à son époque de nombreux adeptes. Ils ne pouvaient donc admettre qu’une quelconque force « occulte » influât à distance sur le mouvement d’un corps matériel.
Quand Descartes décède en 1650, Isaac Newton (1643-1727) n’est qu’un enfant, mais moins de deux décennies plus tard, en postulant une mystérieuse « force de gravité » qui serait à l’origine de toute la dynamique cosmique, le savant anglais allait renverser la magistrale cosmologie tourbillonnaire du Français. La supériorité de la théorie de Newton, qui finit par emporter l’adhésion de la communauté savante dans les premières décennies du xviiie siècle, réside également dans le fait qu’elle affronte une question, demeurée comme un point aveugle de la cosmologie cartésienne : la mathématisation des lois du cosmos. L’univers cartésien est fondamentalement instable. Les tourbillons s’entrechoquent en transférant l’un dans l’autre de la matière qui perturbe en permanence le cours des éléments qui les constituent. Tourbillons, étoiles, planètes, comètes apparaissent et disparaissent. Les trajectoires des objets célestes se heurtent en permanence à l’inertie du milieu ambiant et aux mouvements des corps qui le composent. Vitesse des astres, période de leur révolution ou même tracé de leur orbite s’accordent mal avec des équations ou des figures géométriques simples. En cela, Descartes est bien en deçà des avancées de Kepler, dont il ignore superbement les trois lois mathématiques de la nouvelle dynamique cosmique, énoncées pourtant une bonne génération avant ses propres publications68. Newton en revanche, armé il est vrai des ressources du calcul différentiel et intégral, les a prises en compte en les accordant, dans sa théorie, avec les lois physiques du mouvement établies par Galilée. Il allait ainsi bien plus loin que ne l’avait fait Descartes dans sa tentative de réunir physique et astronomie…
Faut-il conclure qu’après Newton, on en avait fini avec les tourbillons cosmiques remis à l’honneur par Descartes ? Il ne faudrait pas oublier qu’autour de Malebranche, mais aussi de Leibniz, le concept de tourbillon continue de trouver des adeptes, en essayant de s’accorder avec les données nouvelles de la science69. Il ne faudrait surtout pas oublier que l’astronomie contemporaine est loin de les avoir bannis de ses cadres de réflexion lorsqu’elle tente d’expliquer les fondements de la dynamique de l’univers, aussi bien celle des constellations que celle des nombreux systèmes planétaires que postulait Descartes et qui rivalisent depuis peu avec le système solaire, le seul que Descartes avait la capacité d’observer de son vivant.