1. Introduction
La gravitation – selon la terminologie actuelle – est une des quatre forces fondamentales du « Modèle standard »1, élaboré dans les années 1970, trois siècles après la publication en 1687 des Principes mathématiques de la philosophie naturelle d’Isaac Newton (1643-1727)2. Son contenu s’inscrit dans un continuum de pensée, mais constitue aussi une rupture épistémologique. Il s’agit d’un moment majeur dont il n’est pas possible dans un article de le traiter avec exhaustivité, mais que nous tenterons de cerner dans une double perspective, historienne et historiographique, en dégageant les points saillants et spécifiques à l’origine d’un processus qui révolutionne une philosophie naturelle3 dont les bases du paradigme aristotélico-ptoléméen physico-cosmique sont ébranlées par la conceptualisation et la diffusion d’un cosmos héliocentrique (De revolutionibus orbium cœlestium, 15434), la formulation du principe d’équivalence et la mathématisation des lois de la nature par Galilée5, la conceptualisation d’un système solaire où la Lune et les planètes ne sont plus et pas enchâssées dans des orbes de cristal (observations de la comète de 1577 par Tycho Brahe et Thaddæus Hagecius6), et où, d’autre part, les corps se meuvent dans des orbites elliptiques avec une révolution périodique (lois de Kepler 1609-16197). La philosophie naturelle de la première moitié du xviie siècle est aussi profondément renouvelée par les contributions de Gottfried Wilhelm Leibniz (1646-1716), notamment sur les mouvements des corps célestes8 et de René Descartes (1596-1650) qui conçoit un système solaire mécaniste rempli de tourbillons d’éther où les corps célestes sont portés et emportés9.
La physique newtonienne [cinématique, statique et dynamique], de nos jours la mécanique classique – force de gravitation/attraction universelle, et mécanique céleste/lois du mouvement10 – s’élabore dans le contexte intellectuel de la seconde moitié du xviie et de la première du siècle des Lumières, période où se met en place et se développe un processus de transition et de rupture à la fois avec un socle de connaissances qui, à travers des sauts épistémologiques, constitue un nouveau paradigme11. Ceci se fait concomitamment avec un processus de révolution scientifique et qui, au final, aboutit à l’émergence d’une nouvelle science normale12. L’apport de Newton dans les connaissances et conceptions de notre système solaire, à partir de la décennie 1680, constitue un moment majeur par la formalisation de la gravitation comme une force d’attraction qui agit à distance entre les corps indépendamment de leur nature. Mais cette nouvelle physique énoncée par Newton est source de débats et de conflits en Europe, et tout particulièrement en France13, entre les partisans du newtonianisme, du cartésianisme et du leibnizianisme, notamment quant à la nature de la gravitation et à propos de l’éther14.
2. Élaboration et conceptualisation (1661-1687)
Après avoir fréquenté la grammar school de Grantham, c’est au Trinity College, à Cambridge, qu’à partir de 1661 Isaac Newton poursuit ses études et est formé à la philosophie naturelle. L’enseignement dispensé au sein de cette matrice intellectuelle repose sur la rhétorique, la logique, l’éthique et la physique encore très largement inscrites dans le paradigme aristotélicien. À ces savoirs s’ajoutent les lectures faites par Newton tout particulièrement des œuvres de Descartes et des mathématiciens François Viète (1540-1603) et John Wallis (1616‑1703). Parmi ses professeurs, signalons le mathématicien Isaac Barrow (1630-1677) qui occupe une place essentielle dans la formation intellectuelle de Newton et à qui il succède comme professeur de mathématiques en 1669. En janvier 1665 Newton obtient le titre de bachelier ès arts de l’université de Cambridge, ville que menace la grande peste et qu’il quitte pour regagner Woolsthorpe, où se trouve la maison de naissance de Newton.
2.1. 1666 : « Il doit y avoir un pouvoir d’attraction dans la matière »
L’année 1666 est celle du désormais célèbre épisode de la pomme que relate William Stukeley dans Memoirs of Sir Newton’s Life sur la base d’un entretien le 15 avril 1726 :
Après le dîner, le temps étant chaud, nous sommes allés dans le jardin et avons bu du thé à l’ombre de quelques pommiers, seulement lui et moi. Parmi d’autres discours, m’a-t-il dit, il était juste dans la même situation que lorsque jadis, la notion de gravitation lui était venue à l’esprit. « Pourquoi cette pomme devrait-elle toujours descendre perpendiculairement au sol ? », se dit-il ; et à la faveur de la chute d’une pomme, alors qu’il était assis dans une humeur contemplative : « Pourquoi ne devrait-elle pas aller latéralement ou vers le haut ? Mais constamment au centre de la terre ? Assurément, la raison en est que la terre l’attire. Il doit y avoir un pouvoir d’attraction dans la matière et la somme du pouvoir d’attraction de la terre doit être au centre de celle-ci, pas de n’importe quel côté de la terre. Donc cette pomme tombe perpendiculairement, ou vers le centre. Si la matière attire ainsi la matière ; elle doit être proportionnelle à sa quantité. Donc la pomme attire la terre, ainsi que la terre attire la pomme. »
Qu’il existe une force [power] comme celle que nous appelons ici la gravité qui s’étend à travers l’univers et ainsi, par étapes, il a commencé à appliquer cette propriété de la gravitation au mouvement de la terre et des corps célestes : à considérer leurs distances, leurs grandeurs, leurs révolutions périodiques ; à découvrir que cette propriété, conjuguée à un mouvement progressif qui leur était imposé au début, résolvait parfaitement leurs cours circulaires ; empêchait les planètes de tomber les unes sur les autres ou de tomber toutes ensemble dans un centre et ainsi il a dévoilé l’Univers. Ce fut la naissance de ces découvertes étonnantes, par lesquelles il a construit la philosophie sur une base solide, au grand étonnement de toute l’Europe15.
Quoi qu’il en soit de la réalité historique de cet événement, l’année 1666 est considérée depuis le poème de John Dryden comme l’annus mirabilis dans la vie scientifique de Newton16. Elle constitue un tournant épistémologique dans la conceptualisation de la force de gravitation ou d’attraction universelle – universelle car elle s’applique à la totalité des éléments qui composent la Terre (monde terrestre sublunaire de la physique d’Aristote) et s’étend à l’ensemble de l’univers ou cosmos (monde supralunaire aristotélicien) – ainsi que l’émergence d’une mécanique céleste – le ciel est régi par des corps en mouvement17.
2.2. Hooke et Newton : émergence et élaboration du concept d’attraction entre simultanéité et rivalité
Si les trois lois de Kepler décrivent les caractéristiques des mouvements des planètes dans un système héliocentrique, outre Newton, cette question intéresse d’autres savants et, entre autres membres de la Royal Society, Christopher Wren (1632-1723)18, Edmund Halley (1656-1742) et Robert Hooke (1635-1703)19. Ce dernier écrit, en 1666, un article « concernant l’inflexion d’un mouvement direct dans une courbe par un principe attractif »20. Il se demande « pourquoi les planètes se déplacent autour du Soleil comme l’a supposé Copernic, et non pas en ligne droite comme tous les corps qui ont reçu une impulsion doivent le faire » ? Et d’émettre l’hypothèse que « la cause responsable de l’infléchissement du mouvement rectiligne en un mouvement curviligne pourrait résulter de la présence d’un corps attractif placé au centre [le Soleil]. » Hooke se démarque des partisans de la c – la force centrifuge – à l’instar de Christian Huygens21 et de Newton22.
En 1674, dans un article intitulé “An Attempt to Prove the Motion of the Earth from Observations”, Hooke apparaît partisan de la loi de l’inertie et souscrit à la théorie d’une attraction mutuelle qu’il nomme “attractive power”, “attraction” ou “gravitating power” des “cœlestial bodies” [Terre, Lune et planètes] et du Soleil :
Je me suis souvent demandé pourquoi, en suivant la supposition de Copernic, les planètes devraient se déplacer autour du Soleil en n’étant pas incluses dans des orbes solides (ce que les anciens, peut-être pour cette raison, pouvaient admettre) ; ni en n’étant pas liées à lui, comme à leur centre, par quelques cordes visibles ; ni en ne s’écartant pas au-delà de tel ou tel degré ; ni encore en ne se déplaçant pas en ligne droite, comme tous les corps qui n’ont reçu qu’une seule impulsion devraient le faire. Parce qu’un corps solide, déplacé dans un fluide vers n’importe quelle partie (à moins qu’il ne soit poussé de côté par l’impact d’un corps voisin ; ou qu’il ne soit empêché dans ce mouvement par d’autres corps lui faisant obstacle ; ou que le milieu au travers duquel il se déplace ne soit supposé n’être également pénétrable dans toutes les directions) doit persévérer dans son mouvement en ligne droite et ne s’en écarter en aucune manière que ce soit. Or tous les corps célestes, qui sont des corps solides réguliers, se déplaçant dans un fluide, mais en le faisant en suivant des trajectoires circulaires ou elliptiques, mais non droites, doivent avoir, en plus de la première impulsion reçue, une autre cause qui les oblige à incurver leur mouvement. Et pour arriver à ce résultat, je ne peux imaginer aucune autre cause probable en plus de ces deux-ci. La première pourrait provenir d’une densité inégale du milieu que traverse le corps planétaire en se déplaçant ; c’est-à-dire que, si l’on suppose cette partie du milieu ambiant qui est la plus éloignée du centre, ou du soleil, plus dense à l’extérieur que ce qui est plus près, il s’ensuivra que le mouvement direct sera toujours dévié vers l’intérieur par la plus grande pénétrabilité de la partie interne de ce milieu et la plus forte résistance de l’externe. Il y a quelques probabilités qu’il en soit ainsi, en ceci que si l’éther a quelque peu la nature de l’air, il est rationnel que la partie la plus proche du Soleil, la fontaine de chaleur, doive être la plus raréfiée et par conséquent que celles qui sont les plus éloignées doivent être les plus denses, Mais une telle supposition entraîne aussi des improbabilités, dont je ne ferai pas état, car n’apportant rien à mon propos actuel.
Mais la deuxième cause de l’infléchissement d’un mouvement direct vers une courbe peut résulter d’une propriété attractive du corps placé au centre, par laquelle il s’efforce continuellement de l’attirer ou de le diriger vers lui. Car si un tel principe est supposé, il semble possible d’expliquer tous les phénomènes des planètes par le principe commun des mouvements mécaniques ; et il se pourrait que la poursuite de cette spéculation nous donne une véritable hypothèse de leur mouvement, et que d’un petit nombre d’observations, leurs mouvements puissent être portés jusqu’à un si haut degré de certitude, que nous soyons capables de les calculer avec la plus grande exactitude et certitude que l’on puisse désirer23.
Néanmoins Hooke ne parvient pas à formuler une loi de cette attraction mutuelle24. Une querelle éclate avec Newton quand, en 1678, Hooke, en tant que secrétaire de la Royal Society, constate dans le résumé des Principia rédigé par Halley que Newton affirme qu’entre deux corps l’attraction est inversement proportionnelle au carré de la distance entre leurs centres. Hooke réclame l’antériorité et la paternité de cette affirmation25. La controverse prend de l’ampleur et se poursuit dans une correspondance (1679-1680) dont la courtoisie de façade cache une réelle rivalité26. Finalement, Newton publie les Principia en y faisant disparaître le « clarissimus Hookius » (le « très brillant Hooke »).
2.3. La trajectoire des comètes ?
Dans la seconde moitié du xviie siècle, de « grandes comètes »27 sont visibles et sont observées avec acuité par les astronomes qui disposent désormais d’instruments optiques et astrométriques de grande précision28. Parmi les savants qui ont observé la comète de 1682, Edmund Halley s’interroge sur la trajectoire de ces corps : trajectoire linéaire comme le pense Kepler, ou bien trajectoire circulaire à l’instar des planètes comme le soutient Giovanni Domenico Cassini29 ? Halley interroge aussi Newton quant à la forme de l’orbite des comètes et ce dernier d’affirmer qu’elles sont, selon ses propres calculs, elliptiques et non circulaires. En novembre 1684 Newton rédige et transmet à Halley le De motu corporum in gyrum [Sur le mouvement des corps en orbite]30 dont le contenu constitue les prolégomènes des Principia et de la gravitation universelle. Newton y démontre géométriquement que si un corps se meut dans un mouvement elliptique et où un des foyers de cette orbite est le centre attracteur alors le corps est soumis à une force 1/r².
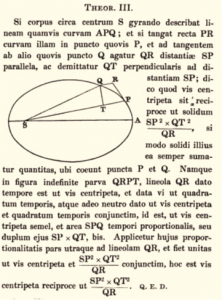
Fig. 1. Théorème 3 du De Motu
Le troisième théorème du De Motu évalue maintenant la force centripète dans une orbite elliptique dont la courbure est considérée comme composée d’arcs infinitésimaux, et la force centripète en tout point est évaluée à partir de la vitesse et de la courbure de l’arc infinitésimal local. Ce point se retrouve dans les Principia : proposition 6 du livre 1. (Rigaud S. P., Historical essay on the first publication of sir Isaac Newton’s Principia, Oxford, University Press, 1838, appendix p. 4)
Domaine public
3. Publication des Principia et diffusion du newtonianisme
L’histoire de cette philosophie est fort courte, les principes n’en furent publiés qu’en 1686, par l’auteur […] ensuite publiés de nouveau en 1713, avec des augmentations considérables. En 1726, un an avant la mort de l’auteur, on donna encore une nouvelle édition de l’ouvrage qui les contient, & qui est intitulé Philosophiæ naturalis principia mathematica, ouvrage immortel, & un des plus beaux que l’esprit humain ait jamais produits31.
3.1. La première édition des Principia (1687)
La première édition des Principia est publiée en 1687, à Londres, au format in-quarto, en latin – signe d’une permanence malgré l’essor croissant des publications en langues nationales au cours du xviie siècle – et selon les estimations à 750 exemplaires32. Cette publication s’inscrit dans un contexte d’institutionnalisation et de normalisation des sciences britanniques33 : au printemps 1686 la Royal Society reçoit une demande de publication des Principia, le 19 mai Halley demande et obtient l’approbation des membres de l’institution ; Halley s’engage aussi à financer la publication dont l’impression est confiée à Joseph Streater et Samuel Smith (Jussu Societatis Regiae ac Typis Josephi Streater. Prostat Venales apud Sam. Smith ad insigna Principis Walliae in Coemiterio D. Pauli, aliosq, nonnullos Bibliopolas). Le 5 juillet 1687, l’ouvrage paraît avec l’imprimatur de « S. Peppys, Reg[alis]. Soc[ietatis]. PRÆSES34 ».
Fig. 2. Couverture de la première édition des Principia, Bnf
Domaine public, BnF
L’ouvrage, dont la publication constitue un moment majeur de débats, controverses et de rupture dans la formation d’une pensée scientifique moderne, est structuré en trois livres qui reflètent la construction du concept de gravitation, des notions (force, espace…) et plus globalement de la mécanique céleste35 :
— De motu corporum : liber primus (« Sur le mouvement des corps : livre premier »), où Newton présente les trois lois du mouvement des corps et définit notamment les concepts de force centripète et de masse.
— De motu corporum : liber secundus (« Sur le mouvement des corps : livre second »), dont le contenu concerne la mécanique des fluides, la friction dans le mouvement des corps, l’existence d’une force qui agit à distance.
— De mundi systemate : liber tertius (« Sur le système du monde : livre troisième »).
C’est dans les Principia que Newton formule quatre lois mathématiques qui régissent la mécanique céleste :
— Loi de la gravitation universelle : Deux corps quelconques s’attirent en raison directe de leur masse et en raison inverse du carré de la distance de leurs centres de gravité.
— Première loi de Newton ou principe de l’inertie (initialement formulée par Galilée) : Dans un référentiel galiléen, le centre d’inertie G d’un solide soumis à un ensemble de forces dont la somme vectorielle est nulle est soit au repos, soit animé d’un mouvement rectiligne et uniforme (le vecteur vitesse demeure constant).
— Deuxième loi de Newton (ou théorème du centre d’inertie) : Dans un référentiel galiléen, la somme vectorielle des forces appliquées à un objet ponctuel est égale au produit de la masse de l’objet par son vecteur accélération.
— Troisième loi de Newton : Lorsqu’un solide S1 exerce une force sur un solide S2, le solide S2 exerce sur le solide S1, la force directement opposée.
3.2. Les éditions successives (1713 et 1726)
Newton, président de la Royal Society (1703-1727) et désormais engagé depuis 1689 dans une carrière politique et administrative, publie deux autres éditions des Principia avec la mention « aucta et emendata » (« revue et complétée ») : en 1713, à Cambridge, et une dernière, en 1726, à Londres, un an avant la mort de l’auteur. La seconde édition est motivée à la fois par la rareté de l’ouvrage36, par le désir de Newton en personne qui a accumulé des annotations pour en réviser le contenu37 et est mise sous presse par le truchement de son entourage et de ses correspondants, comme Richard Bentley (1662-1742) et Roger Cotes (1692-1716).
Fig. 3. Préface de la seconde édition des Principia
Préface de Newton de la seconde édition in, Principes mathématiques, vol. 1, p. xix., d’après la version française d’Émilie du Châtelet
Domaine public, BnF
Outre les chapitres mis à jour, cette nouvelle édition, imprimée à 750 exemplaires, comprend un Scholium generale où, répondant aux critiques de la première édition, il affirme : Hypotheses non fingo (« Je ne formule aucune hypothèse ») ! Dans le Scholium Newton répond tout particulièrement aux objections faites à sa théorie qui serait un retour aux « forces occultes » de la physique aristotélicienne et il critique la théorie des tourbillons cartésiens incompatibles avec les orbites très excentriques des comètes.
La troisième édition a été publiée en 1726 à 800 exemplaires sous la direction de Henry Pemberton (1694-1771) et par l’imprimerie londonienne de Guil. [William] et John Innys38. Il s’agit de la dernière édition aucta et emendata par Newton alors que celui-ci, âgé de 83 ans, s’est plus ou moins éloigné depuis une vingtaine d’années des questions scientifiques et notamment de la physique. Son contenu est considéré comme la référence de l’œuvre de Newton, c’est l’édition sur laquelle Alexandre Koyré et I. Bernard Cohen ont travaillé39.
3.2. Diffusion, traduction et vulgarisation des Principia dans le monde européen
Parallèlement aux nouvelles éditions de 171340 et 1726, les Principia sont publiés à Amsterdam, toujours en latin, en 1714 et 1723, ces deux éditions in quarto reprennent le texte amendé de 1713. Le nombre somme toute limité d’impressions de l’ouvrage au regard du lectorat est sans nul doute à l’origine des publications faites à Amsterdam41, qui est à la fois une des villes intellectuelles du continent et un important centre d’impression. C’est aussi aux Pays-Bas que s’illustre Willem Jacob ’s Gravesande (1688-1742), un des fondateurs du Journal littéraire de La Haye, engagé dans le conflit qui oppose Newton et Leibniz. ‘s Gravesande est un des premiers savants du continent à adhérer au newtonianisme42. En 1715, alors qu’il se trouve à Londres avec l’ambassade des États généraux des Provinces-Unies, il fréquente les milieux scientifiques de la capitale partisans de l’attraction universelle. En 1719, il publie à Leyde les Physices elementa mathematica experimentis confirmata, sive introductio ad philosophiam Newtonianam, qui sont réédités en 1725, et 174243 ; puis, en 1723, les Philosophiae Newtonianae Institutiones, in usus academicos44. Plus largement, il apparaît que l’université de Leyde est à l’échelle continentale un foyer de diffusion de la théorie newtonienne et, sans nul doute, le premier chronologiquement et par la caution intellectuelle qu’elle lui apporte.
C’est en 1726 que la troisième édition des Principia est traduite en anglais par Andrew Motte (1696-1734) et est publiée, en 1729, par son frère et éditeur Benjamin Motte (1693-1738)45. Puis entre 1745 et 1745, Émilie du Châtelet (1706-1749)46 traduit les Principia en français qui sont publiés une première fois en 1756 et, dans une version définitive, en 1759. Enfin, en 1770, les Principia sont traduits en langue espagnole par José Celestino Mutis (1732-1808) qui introduit la physique newtonienne dans l’Amérique espagnole47. Ces traductions sont à considérer en tant que vecteurs de diffusion des Principia dans le monde savant des Lumières et dans les territoires sous domination impériale des Amériques, et en creux les aires culturelles à l’écart à la fin du xviiie siècle48.
En France, l’édition du 2 août 1688 du Journal des Sçavans annonce la publication des Principia et le contenu de l’article montre un évident scepticisme quant à la valeur scientifique du livre et c’est en France, du fait de l’impact du cartésianisme, que les résistances ont été les plus fortes :
L’ouvrage de Monsieur Newton est une Mecanique la plus parfaite qu’on puisse imaginer […]. Mais il faut avouër qu’on ne peut regarder ces demonstartions que comme mecaniques, puisque l’auteur reconnoit lui-mesme […] qu’il n’a pas consideré leurs principes en Physicien, mais en simple Geometre […].
Pour faire donc un ouvrage le plus parfait qu’il est possible, Mr. Newton n’a qu’à nous donner une Physique aussi exacte qu’est la Mecanique. Il l’aura donnée quand il aura substitué de vrais mouvemens en la place de ceux qu’il a supposez49.
Néanmoins la diffusion du newtonianisme se fait par une littérature à la fois de vulgarisation et savante50, qui connaît un fort essor à partir du milieu de la décennie 1730, et cela à travers les journaux et des ouvrages51, de défense ou d’opposition. Les écrits de Voltaire ont joué un rôle très important dans la vulgarisation des théories de Newton52, de même que ceux de Francesco Algarotti (1712-1764)53. Quant à ceux des jésuites Noël Regnault (1683-1762)54 et Louis Castel (1688-1757)55, des minimes Thomas Le Seur (1703-1770) et François Jacquier Genève (1711-1788)56, ou encore de Charles-François Roland Le Virloys (1716-1772)57, ils s’inscrivent dans une entreprise savante de diffusion et de commentaire. En 1763, alors que la physique newtonienne s’impose dans le monde savant et les institutions scientifiques, le jésuite Aimé-Henri Paulian publie le Traité de paix entre Descartes et Newton, où il fait la proposition suivante :
Pour faire connaître et pour réconcilier ces deux grands Hommes, je donnerai d’abord leurs Vies littéraires avec toute l’étendue et toute la critique dont elles sont susceptibles ; j’exposerai ensuite avec toute la franchise possible les erreurs qu’ils ont enseignées, et les vérités qu’ils ont découvertes ; je proposerai enfin un système mixte d’où les unes seront exclues, et où les autres seront heureusement alliées58.
Fig. 4. Illustration et page de titre des Éléments de la philosophie de Neuton
Domaine public, BnF
4. Confirmation et succès d’une révolution scientifique
C’est au cours de la première moitié du siècle des Lumières que les théories newtoniennes sont confirmées et que, après des îles Britanniques, les institutions scientifiques et savants du continent, inscrits dans le cartésianisme ou le leibnizianisme, adhèrent à la théorie de la gravitation universelle. Ce fut par une mathématisation et tout particulièrement dans le royaume de France, où les très cartésiens Cassini et Fontenelle dominent les institutions savantes (direction de l’Observatoire et secrétariat perpétuel de l’Académie des sciences), que des expériences commanditées par l’Observatoire royal de Paris et l’Académie royale des Sciences contribuent à montrer que la forme de la Terre ainsi que le retour de la comète observée en 1682 s’inscrivent dans le paradigme de la physique de Newton.
4.1. La forme de la Terre : les expéditions du Pérou (1735-1745) et de Laponie (1736-1737)
Dans la décennie 1730, la question de la forme de la Terre connaît un regain d’intérêt et oppose les tenants de la physique cartésienne des tourbillons aux partisans de la gravitation universelle, les premiers affirmant que la Terre est aplatie au niveau de l’équateur alors que pour les seconds c’est au niveau des pôles59. Pierre Louis Moreau de Maupertuis (1698-1759), qui parmi les académiciens royaux des sciences se déclare ouvertement newtonien, est sans nul doute un des plus ardents défenseurs de cette dernière vision de notre planète60.
Une force secrète qu’on appelle pesanteur attire ou chasse les Corps vers le centre de la Terre. Cette force, si on la suppose par tout la même, rendrait la Terre parfaitement sphérique, si elle était composée d’une matière fluide et homogène, et qu’elle n’eût aucun mouvement : car il est évident qu’afin que chaque colonne de ce fluide, prise depuis le centre jusqu’à la superficie, demeurât en équilibre avec les autres, il faudrait que son poids soit égal au poids de chacune des autres ; et puisque la matière est supposée homogène, il faudrait pour que le poids de chaque colonne fût le même, qu’elles fussent toutes de même longueur. Or il n’y a que la Sphère, dans laquelle cette propriété se puisse trouver ; la Terre serait donc parfaitement sphérique.
Mais c’est une Loi pour tous les Corps qui décrivent des Cercles, de tendre à s’éloigner du centre du Cercle qu’ils décrivent, et cet effort qu’ils font pour cela, s’appelle force centrifuge ; l’on sait encore que si des Corps égaux décrivent dans le même temps des Cercles différents, leurs forces centrifuges sont proportionnelles aux Cercles qu’ils décrivent. Si donc la Terre vient à circuler autour de son axe, chacune de ses parties acquerra une force centrifuge, d’autant plus grande que le Cercle qu’elle décrira sera plus grand, c’est-à-dire, d’autant plus grande, qu’elle sera plus proche de l’Equateur, cette force allant s’anéantir aux Pôles61.
En 1735, la querelle quant à la forme de la Terre est telle que l’Académie royale des Sciences, largement dominée par les opposants au newtonianisme, décide d’organiser, avec le soutien du ministre de la Marine Maurepas, deux expéditions scientifiques successives pour mesurer le degré méridien à deux latitudes extrêmes. La première doit se rendre dans l’Amérique équinoxiale pour effectuer une mesure au niveau de l’équateur, expédition géodésique franco-espagnole dans la Vice-royauté du Pérou, composée notamment par les savants français Pierre Bouguer (1698-1758) et Charles Marie de La Condamine (1701-1774)62 qui sont accompagnés par Jorge Juan y Santacilia (1713-1773) et Antonio de Ulloa (1716-1795), deux scientifiques espagnols ilustrados et acquis aux théories newtoniennes63. La seconde a pour destination la Laponie dans le but d’y réaliser des opérations géodésiques au niveau du cercle polaire sous la direction du très newtonien Maupertuis. Le 28 août 1737, de retour de Laponie, Maupertuis annonce que le degré méridien mesuré en Laponie est plus long que celui mesuré en France – le « degré Picard » – et donc la Terre est aplatie aux pôles et inversement renflée à l’équateur : Newton a raison ! Les résultats de l’expédition en Équateur sont annoncés en 1744 et confirment cela, tout comme les mesures réalisées dans le cadre de la « Méridienne Vérifiée » (1739-1740).
4.2. Le calcul du retour de la comète de Halley
Halley, dans A Synopsis of the Astronomy of Comets (1705) et selon les théories cométaires de Newton (orbite elliptique et loi de la gravitation), écrit :
Ainsi, chaque fois qu’une nouvelle comète apparaîtra, nous serons peut-être en mesure de savoir, en comparant ensemble les éléments, s’il s’agit de ceux qui sont apparus auparavant et, par conséquent, de déterminer sa période, et l’axe de son orbite, et de prédire son retour. Et, en effet, il y a beaucoup de choses qui me font croire que la comète qu’Apian a observée en l’an 1531 était la même que celle que Kepler et Longomontanus ont étudiée et décrite en l’an 1607, et que j’ai moi-même vu revenir et que j’ai observée en l’an 168264.
Halley calcule, en prenant en compte l’action de Jupiter, que la comète revient tous les 75 à 76 ans et annonce son retour pour une période allant de la fin de 1758 au de 175965. Après la mort de Halley en 174266, et le retour prédit se rapprochant, plusieurs savants tentent de calculer précisément le passage au périhélie. Parmi ceux-ci se signalent Leonhard Euler (1707-1783), Jean Philippe Loys de Cheseaux (1718-1751) et un groupe formé par Alexis Clairaut (1713‑1765)67, Joseph Jérôme de Lalande (1732-1807) et Nicole-Reine Lepaute (1723-1788)68. Le 14 novembre 1758, devant l’Académie royale des Sciences, Clairaut annonce que le passage du périhélie aura lieu mi-avril 1759. Si finalement la comète passe au périhélie un mois plus tôt, le 13 mars, Lalande déclare, le 25 avril, devant l’Académie royale des Sciences, que ce retour de la comète « change nos doutes en certitudes, et nos hypothèses en des démonstrations 69 ».
4.3. Le paradigme newtonien et la « science normale »
Avec Pierre-Simon de Laplace70, la physique newtonienne trouve dans le Traité de mécanique céleste71 l’archétype du savant « normal »72 qui s’est inscrit sans le discuter dans le legs des Principia et dont l’œuvre scientifique fut de confirmer la théorie de la gravitation dans un programme de recherche.
Newton publia, vers la fin du dix-septième siècle, la découverte de la pesanteur universelle. Depuis cette époque, les géomètres sont parvenus à ramener à cette grande loi de la nature, tous les phénomènes connus du système du monde, et à donner ainsi aux théories et aux tables astronomiques, une précision inespérée. Je me propose de présenter sous un même point de vue ces théories éparses dans un grand nombre d’ouvrages, et dont l’ensemble embrassant tous les résultats de la gravitation universelle, sur l’équilibre et sur les mouvements des corps solides et fluides qui composent le système solaire et les systèmes semblables répandus dans l’immensité des cieux, forme la Mécanique céleste. L’Astronomie, considérée de la manière la plus générale, est un grand problème de Mécanique, dont les éléments des mouvements célestes sont les arbitraires ; sa solution dépend à la fois de l’exactitude des observations et de la perfection de l’analyse, et il importe extrêmement d’en bannir tout empirisme, et de la réduire à n’emprunter de l’observation, que les données indispensables. […] Je donnerai les méthodes et les formules pour déterminer les mouvements des centres de gravité des corps célestes, la figure de ces corps, les oscillations des fluides qui les recouvrent, et leurs mouvements autour de leurs propres centres de gravité73.
Trois grands axes structurent le programme de recherche laplacien pour montrer que les irrégularités observées s’expliquent par une prise en compte de toutes les interactions gravitationnelles, pour fixer le statut de la loi de la gravitation quant à l’existence d’un « éther » et de l’échelle de son action (échelle du système solaire et échelle moléculaire ?), et enfin répondre à la question de la stabilité du système solaire.
5. Conclusion
« Nous n’avons rien à ajouter à cet article sur l’exposition de la philosophie newtonienne, sinon de prier le lecteur de ne point en séparer la lecture de celle des mots Attraction & Gravité. » (Jean le Rond d’Alembert). Si au mitan du siècle des Lumières dans l’Encyclopédie, d’Alembert écrit dans l’article « Newtonianisme » de l’Encyclopédie74 qu’il n’a « rien à ajouter […] sur l’exposition de la philosophie newtonienne, sinon de prier le lecteur de ne point en séparer la lecture de celle des mots Attraction & Gravité » et que « l’histoire de cette philosophie [de Newton] est fort courte », les théories newtoniennes constituent un moment majeur de la pensée scientifique de ce siècle qui, dans une perspective historique, peut se caractériser comme un saut épistémologique radical avec la théorie de la force d’attraction/gravité et une révolution scientifique concomitamment à la constitution du paradigme d’une science normale : la mécanique céleste classique des différents corps du système solaire75.
Au xixe siècle, deux « anomalies » se posent à propos de la théorie classique de la gravitation : irrégularités de l’orbite d’Uranus et précession du périhélie de Mercure. À la lumière des différents calculs quant au mouvement d’Uranus, François Arago émet l’hypothèse d’une perturbation causée par l’attraction d’une planète inconnue, conformément aux lois de Newton. Dans le même temps et par des calculs, Urbain Le Verrier76 et John Couch Adams déterminent la position de cette hypothétique planète. Le 23 septembre 1836, Johann Gottfried Galle, informé par le premier, et Heinrich Louis d’Arrest observent le corps perturbateur : Neptune. Mais les observations astronomiques montrent aussi que l’orbite de Mercure présente des irrégularités : le périhélie se déplace ! Selon les lois de la mécanique céleste, ce phénomène devrait être le résultat d’une perturbation gravitationnelle causée par une hypothétique planète inframercurielle : la planète Vulcain77. Le Verrier en calcule l’orbite et en donne les éléments en 1859. Malgré les observations et les faux espoirs de découverte, point de planète Vulcain. Finalement, les mouvements de Mercure ne sont expliqués qu’en 1915 par la relativité générale d’Albert Einstein78. Plus récemment, dans les années cinquante et soixante, la gravitation est questionnée quant à la gravitation répulsive79.